Pada tutorial kali ini Konsep Koding akan mulai berbagi mengenai dasar Machine Learning Bahasa Indonesia. Pada series kali ini kita akan mempelajari basic Linear Algebra dan dasar-dasar fundamental Machine Learning Bahasa Indonesia. Pada tutorial ini kita akan mempelajari menegnai Scalar, Vector, Matrix dan Tensor pada Linear Algebra yang berfungsi untuk dara kecerdasan buatan atau Machine Learning.
Kenapa kita harus mempelajari Linear Algebra (Scalar, Vector, Matrix dan Tensor)?
Aljabar linier, probabilitas, dan kalkulus adalah 'bahasa' yang digunakan untuk menulis pembelajaran mesin. Mempelajari topik ini akan memberikan pemahaman yang lebih dalam tentang mekanisme algoritmik yang mendasari dan memungkinkan pengembangan algoritme baru, yang pada akhirnya dapat digunakan sebagai strategi perdagangan kuantitatif yang lebih canggih.
Banyak algoritma pembelajaran mesin dan pembelajaran mendalam yang diawasi sebagian besar memerlukan pengoptimalan fungsi kerugian dengan menyesuaikan parameter model. Untuk melakukan ini diperlukan beberapa gagasan tentang bagaimana fungsi kerugian berubah karena parameter model divariasikan.
Ini segera memotivasi kalkulus — topik dasar dalam matematika yang menjelaskan perubahan besaran terhadap yang lain. Secara khusus, ini membutuhkan konsep turunan parsial, yang menentukan bagaimana fungsi kerugian diubah melalui perubahan individual di setiap parameter.
Turunan parsial ini sering dikelompokkan bersama — dalam matriks — untuk memungkinkan penghitungan yang lebih mudah. Bahkan model pembelajaran mesin yang paling dasar seperti regresi linier dioptimalkan dengan teknik aljabar linier ini.
Topik utama dalam aljabar linier adalah tentang vektor dan notasi matriks. Mampu 'membaca bahasa' aljabar linier akan membuka kemampuan untuk memahami buku teks, posting web, dan makalah penelitian yang berisi deskripsi model yang lebih kompleks. Ini tidak hanya memungkinkan reproduksi dan verifikasi model yang sudah ada, tetapi akan memungkinkan ekstensi dan perkembangan baru yang kemudian dapat diterapkan dalam strategi perdagangan.
Banyak algoritma pembelajaran mesin dan pembelajaran mendalam yang diawasi sebagian besar memerlukan pengoptimalan fungsi kerugian dengan menyesuaikan parameter model. Untuk melakukan ini diperlukan beberapa gagasan tentang bagaimana fungsi kerugian berubah karena parameter model divariasikan.
Ini segera memotivasi kalkulus — topik dasar dalam matematika yang menjelaskan perubahan besaran terhadap yang lain. Secara khusus, ini membutuhkan konsep turunan parsial, yang menentukan bagaimana fungsi kerugian diubah melalui perubahan individual di setiap parameter.
Turunan parsial ini sering dikelompokkan bersama — dalam matriks — untuk memungkinkan penghitungan yang lebih mudah. Bahkan model pembelajaran mesin yang paling dasar seperti regresi linier dioptimalkan dengan teknik aljabar linier ini.
Topik utama dalam aljabar linier adalah tentang vektor dan notasi matriks. Mampu 'membaca bahasa' aljabar linier akan membuka kemampuan untuk memahami buku teks, posting web, dan makalah penelitian yang berisi deskripsi model yang lebih kompleks. Ini tidak hanya memungkinkan reproduksi dan verifikasi model yang sudah ada, tetapi akan memungkinkan ekstensi dan perkembangan baru yang kemudian dapat diterapkan dalam strategi perdagangan.
Aljabar linier memberikan langkah-langkah pertama ke dalam vektorisasi, menyajikan cara berpikir yang lebih dalam tentang paralelisasi operasi tertentu. Algoritme yang ditulis dalam notasi 'for-loop' standar dapat dirumuskan ulang sebagai persamaan matriks yang memberikan keuntungan signifikan dalam efisiensi komputasi.
Metode tersebut digunakan di pustaka Python utama seperti NumPy, SciPy, Scikit-Learn, Pandas, dan Tensorflow. GPU telah dirancang untuk menjalankan operasi aljabar linier yang dioptimalkan. Pertumbuhan eksplosif dalam pembelajaran mendalam sebagian dapat dikaitkan dengan sifat sangat paralel dari algoritme yang mendasari pada perangkat keras GPU komoditas.
Aljabar linier adalah subjek matematika kontinu tetapi pada akhirnya entitas yang dibahas di bawah ini diimplementasikan dalam lingkungan komputasi diskrit. Representasi diskrit entitas aljabar linier ini dapat menyebabkan masalah overflow dan underflow, yang mewakili batas-batas secara efektif mewakili angka yang sangat besar dan kecil secara komputasi.
Metode tersebut digunakan di pustaka Python utama seperti NumPy, SciPy, Scikit-Learn, Pandas, dan Tensorflow. GPU telah dirancang untuk menjalankan operasi aljabar linier yang dioptimalkan. Pertumbuhan eksplosif dalam pembelajaran mendalam sebagian dapat dikaitkan dengan sifat sangat paralel dari algoritme yang mendasari pada perangkat keras GPU komoditas.
Aljabar linier adalah subjek matematika kontinu tetapi pada akhirnya entitas yang dibahas di bawah ini diimplementasikan dalam lingkungan komputasi diskrit. Representasi diskrit entitas aljabar linier ini dapat menyebabkan masalah overflow dan underflow, yang mewakili batas-batas secara efektif mewakili angka yang sangat besar dan kecil secara komputasi.
Penjelasan Scalar, Vector, Matrix Dan Tensor
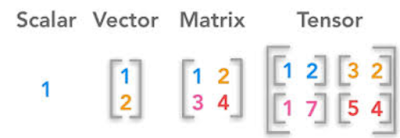 |
| Perbedaan Scalar, Vector, Matrix, Tensor |
Scalars
Skalar adalah bilangan tunggal dan merupakan contoh tensor orde-0. Dalam matematika, perlu untuk mendeskripsikan himpunan nilai yang termasuk dalam skalar. Notasimenyatakan bahwa nilai skalar (huruf kecil) adalah elemen dari (atau anggota dari) himpunan bilangan real, Contoh nya 2
.
Ada berbagai kelompok minat dalam pembelajaran mesin.
mewakili himpunan bilangan bulat positif (). mewakili bilangan bulat, yang mencakup nilai positif, negatif, dan nol.
mewakili himpunan bilangan rasional yang dapat diekspresikan sebagai pecahan dari dua bilangan bulat.
Vektor/Vector
Vektor adalah susunan urutan bilangan tunggal dan merupakan contoh tensor orde-1. Vektor adalah anggota dari objek yang disebut ruang vektor. Sebuah ruang vektor dapat dianggap sebagai kumpulan keseluruhan dari semua vektor yang mungkin dengan panjang (atau dimensi) tertentu. Ruang vektor nilai riil tiga dimensi, dilambangkan dengansering digunakan untuk mewakili gagasan dunia nyata kita tentang ruang tiga dimensi secara matematis.
Secara lebih formal, ruang vektor adalah
-dimensi Cartesian perkalian dari suatu himpunan dengan dirinya sendiri, bersama dengan definisi yang tepat tentang bagaimana menambahkan vektor dan mengalikannya dengan nilai skalar. Jika semua skalar dalam sebuah vektor bernilai riil maka notasi tersebut menyatakan bahwa nilai vektor (huruf tebal huruf kecil) adalah anggota ruang vektor dimensi bilangan real,
.
Terkadang perlu untuk mengidentifikasi komponen vektor secara eksplisit. Itu
Elemen skalar vektor ditulis sebagai. Perhatikan bahwa ini bukan huruf kecil tebal karena elemennya adalah skalar. Sebuah
vektor -dimensi itu sendiri dapat ditulis secara eksplisit menggunakan notasi berikut:
Mengingat bahwa ada skalar untuk merepresentasikan nilai, mengapa vektor diperlukan? Salah satu kasus penggunaan utama vektor adalah untuk merepresentasikan besaran fisik yang memiliki besaran dan arah. Skalar hanya mampu mewakili besaran.
Misalnya skalar dan vektor menyandikan perbedaan antara kecepatan mobil dan kecepatannya. Kecepatan tidak hanya berisi kecepatannya tetapi juga arah perjalanannya. Tidak sulit untuk membayangkan lebih banyak besaran fisik yang memiliki karakteristik serupa seperti gaya gravitasi dan elektromagnetik atau kecepatan angin.
Dalam pembelajaran mesin, vektor sering kali mewakili vektor fitur, dengan masing-masing komponennya menentukan seberapa penting fitur tertentu. Fitur tersebut dapat mencakup kepentingan relatif kata-kata dalam dokumen teks, intensitas sekumpulan piksel dalam gambar dua dimensi, atau nilai harga historis untuk penampang instrumen keuangan.
Vector juga biasa sering disebut dengan Array satu dimensi,
Contoh a = [1,2,3,4]
Matriks
Matriks adalah array persegi panjang yang terdiri dari angka-angka dan merupakan contoh tensor orde-2. Jikadan merupakan bilangan bulat positif, maka matriks tersebut berisi angka, dengan baris dan
kolom.
Jika semua skalar dalam matriks bernilai riil maka matriks dilambangkan dengan huruf tebal kapital, seperti
. Itu adalah matriks tinggal di a
-dimensi ruang vektor bernilai nyata. Oleh karena itu, matriks adalah vektor yang hanya ditulis dengan cara seperti tabel dua dimensi.
Contoh
matriks dapat ditulis sebagai:
Tensor
Entitas yang lebih umum dari suatu tensor merangkum skalar, vektor, dan matriks. Terkadang perlu — baik dalam ilmu fisika dan pembelajaran mesin — untuk menggunakan tensor dengan urutan yang melebihi dua.Dalam fisika teoretis, dan relativitas umum khususnya, tensor kelengkungan Riemann adalah tensor orde-4 yang menggambarkan kelengkungan lokal ruangwaktu. Dalam pembelajaran mesin, dan pembelajaran mendalam khususnya, tensor urutan ke-3 dapat digunakan untuk menggambarkan nilai intensitas beberapa saluran (merah, hijau, dan biru) dari gambar dua dimensi.
Tensor akan diidentifikasi dalam rangkaian posting ini melalui notasi sans-serif huruf tebal,
. Untuk elemen tensor orde-3 akan diberikan oleh, sedangkan untuk elemen tensor orde-4 akan diberikan oleh.
Sekian semoga artikel terkait #1 Pengertian Scalar, Vector, Matrix Dan Tensor Machine Learning dapat bermanfaat dan membantu kamu yang sedang mempelajari fundamental Machine Learning. Pada tutorial selanjutnya kita akan membahas mengenai Numpy.
Baca Juga:



0 Comments